Often heat needs to be extracted from an embedded system to increase lifetime and performance. Heat extracting methods include active and passive heat sink cooling, thermoelectric cooling, water cooling, heat pipes and phase-change cooling. Every method has its advantages and disadvantages.
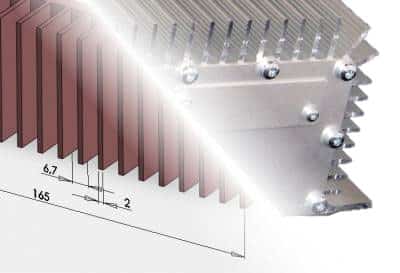
Passive cooling using plate fin sinks is a fail safe and quiet method that consumes no power and is easy to manufacture. This article describes how to use the physics and mathematics behind a plate fin sin sink to design a sufficient cooling device for an embedded system.
The discussion is based on an embedded system with a power consumption of 12 W. The system is mounted in an aluminum casing with a flat 245 mm times 290 mm surface, a suitable place to mount the heat sink. The heat sink is there to keep the system temperature within acceptable levels. An acceptable temperature level in this case is typically between 30 degrees and 50 degrees Celsius depending on hardware and component temperature restrictions.
|
|
|
| Extracting heat by natural convection |
The temperature can only be kept within the limits by extracting heat through conduction, convection or radiation. Plate fin sinks extract heat by natural convection. Heat spreading is essentially area enlarging. The larger the area the more energy can be removed at the same temperature difference.
Unfortunately calculating the natural convection heat transfer for a specific plate fin heat sink is not that simple. A lot of constraints have influence on the heat flow, such as geometry, material properties, and the boundary and ambient conditions. The physics of such a model is described in detail further down in the text.
|
|
|
Web based simulation tool
|
Luckily there are easier ways to perform the calculations. The situation is often simplified in a model where isothermal boundary conditions are assumed to uniformly apply over the back surface of the base plate.The Microelectronic Heat Transfer Laboratory of the Department of Mechanical and Mechatronics Engineering at the University of Waterloo has simulation tools using this particular model to do various calculations on plate fin heat sinks.
|
Click to use web based simulation tool for natural convection »